T 128

Neue reine Temperatur

Bei der Beschreibung der Tonintervall-Quotienten und der zugehörigen Dezimalzahlen ist häufig für die Tonstufe der "großen Sexte" der Quotient 5/3 bzw. die Dezimalzahl 1.666... , für die "kleine Septime"  16/9 bzw. 1.777... angegeben.

Nimmt man für den Oktavenquotienten 2/1 statt der Dezimalzahl 2.0 die definitionsgemäß gleiche Zahl 1.999..., dann bietet sich in dieser Folge als Dezimalzahlen für die Tonstufe der "großen Septime" die Zahl 1.888... an. Umgerechnet entspricht dieser Wert 1101.045 Cent, also einem Wert auf der logarithmischen Cent-Skala, der dicht bei der 1100-Stufe liegt und deshalb musikalisch brauchbar ist (siehe dazu T 31). 1.888... ist zum Quotienten umgerechnet gleich 17/9 und somit ergibt sich für die vier Tonstufen in der chromatischen Folge von großer Sexte bis zur Oktave:

1.999... = 2/1 = 18/9 (Oktave)
1.888... = 17/9 (große Septime)
1.777... = 16/9 (kleine Septime)
1.666... = 5/3 = 15/9 (große Sexte)

Der Tonbereich zwischen „große Terz“ und „große Sexte“ ist so zu unterteilen:
Die Tonstufe "Quinte" liegt mit der Dezimalzahl 1.5 exakt in der Mitte zwischen den Dezimalzahlen 1.333... (Quarte) und 1.666... (große Sexte). Halbiert man den Abstand, der von der Quinte zu den beiden anderen Tonstufen je 0.1666... beträgt, dann ist mit 0.08333...-Schritten eine Folge von Dezimalzahlen entwickelt, für die in der folgenden Tabelle die entsprechenden Tonintervall-Quotienten mit der Zahl 12 im Nenner gleich mitnotiert sind . Die Tonstufe >große Terz< hat in der Folge der Dezimalzahlen zur >Quarte< ebenfalls den Abstand 0.08333... :

1.666... = 5/3 = 20/12 (große Sexte)
1.58333... = 19/12 (kleine Sexte)
1.5 = 3/2 = 18/12 (Quinte)
1.41666... = 17/12 (Tritonus)
1.333... = 4/3 = 16/12 (Quarte)
1.25 = 5/4 = 15/12 (große Terz)

Im Tonbereich zwischen den Tonstufen „Grundton“ (1.0) und „Quinte“ (1.5) liegt in der Mitte mit der Dezimalzahl 1.25 die Tonstufe "große Terz", die Tonstufe "Ganzton" mit 1.125 wiederum genau in der Mitte zwischen „Grundton“ und „große Terz“.
Analog zu den beiden bereits entwickelten Folgen wird auch die dritte komplettiert, indem für die Tonstufen "kleine Terz" und "Halbton" die Dezimalzahlen ebenfalls genau mitten zwischen die Nachbar-Tonstufen gelegt sind. Deren Tonintervall-Quotienten haben diesmal die Zahl 16 im Nenner (die sich ergebenden Tonstufen zwischen „Großterz“ und „Quinte“ werden nicht gebraucht):

1.5 = 3/2 = 24/16 (Quinte)
. . . 23/16 .
. . . 22/16 .
. . . . 21/16 .
1.25 = 5/4 = 20/16 (große Terz)
1.1875 = 19/16 (kleine Terz)
1.125 = 9/8 = 18/16 (Ganzton)
1.0625 = 17/16 (Halbton)
1.0 = 1/1 = 16/16 (Grundton)

Eine kleine Graphik zeigt die Zusammenhänge der genannten Intervallproportionen. Die drei Quotientengruppen sind - ungekürzt - am linken Rand notiert. Die Beziehung zu der mit 12 Tonstufen (im gleichen Abstand) an der Basis der Graphik beschriebene Oktave ist bei der 9-Teilung durch die schräg verlaufenden Strecken gezeigt: dis-c für die Quotienten 15/9 bis 18/9, cis-a für die Quotienten 15/12 bis 20/12 und c-e für die Quotienten 16/16 bis 20/16.

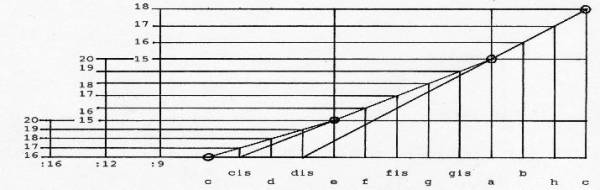
Die Graphik macht deutlich, wie gleichmäßig die Tonstufen innerhalb des Oktavenintervalles verteilt sind.
Die "Kurve", die durch die drei gezeigten Linien (Sekanten der logarithmischen Kurve) beschrieben wird und die durch weitere aus den Nachbaroktaven in beide Richtungen unbegrenzt fortsetzbar ist, zeigt die logarithmische Kurve welche entsteht, wenn auf der Horizontalen stets gleiche Strecken für Tonintervalle (Beispiel Oktaven) genommen werden, während auf der Vertikalen diese Intervalle halbe bzw. doppelte Streckenlänge haben müssen, weil definitionsgemäß die Tonstufe der Oktave zur Grundtonstufe die doppelte Tonfrequenzzahl hat.

Nach den musikalischen Rechenregeln lassen sich aus der vollständigen 12-stufigen Skala für diese Temperatur der komplette Tabellensatz berechnen und die Kennlinien sowie das Profil ableiten:

> Umrechnung in die Cent-Skala:
Die ausdividierten Intervall-Quotienten - das sind die Dezimalzahlen - werden logarithmiert, mit der Zahl 1200 multipliziert und durch die Zahl 0.30103 - das ist log2 - dividiert.
Das Ergebnis "Centwert des Intervalls" wird auf drei Dezimalstellen gerundet (siehe Abschnitt >Genauigkeit<).

> Die vier Cent-Tabellen "Quinten - Quarten - Großterzen - Kleinterzen" geben für jedes genannte Intervall die Differenzen zwischen den sie begrenzenden Tonstufen an.

> Die "Verteilung des pK" ergibt sich aus der soeben berechneten Cent-Tabelle der Quinten-Skala, wenn für jede der zwölf Quinten deren Differenz zur reinen 3/2-Quinte (bzw. 701.955 cent) angegeben wird
Gegebenenfalls sind die Zahlen in der dritten Dezimalstelle so zu ändern, daß die in jedem Fall geforderte Summenzahl 23.460 cent erreicht wird - dieses ist keine verfälschende Korrektur.

> Die "Verteilung des pK im Quintenzirkel" nennt das Tonintervall, um welches die reine 3/2-Quinte vermindert wird, die rein gebliebenen Quinten sind mit "3/2" gekennzeichnet. Auf diese Weise sind die veränderten Quinten durch die Größe der sie verändernden Kleinintervalle beschrieben - so wie es in der musikalischen Literatur üblich ist.
Die individuelle Quintengröße ist als Differenz vom reinen Quintintervall zu errechnen:
Beispiel 1 (u.a. T 14): "reine Quinte" plus "Diaschisma"  -  3/2 x 2048/2025 = 3x2048/2x2025 = 3072/2025
Beispiel 2 (u.a. T 14): "reine Quinte" minus "sK" oder "81/80"  -  3/2 : 81/80 = 3/2 x 80/81 = 3x80/2x81 = 40/27

> Die beiden "Frequenzbeispiele" sind wiederum in der linearen Skala, sie errechnen sich deshalb (ohne Umrechnung in eine logarithmische Skala) direkt aus den Dezimalzahlen: Die Tonfrequenzen in der Oktave auf "a" sind einfache Produkte aus Grundton-Frequenz und Dezimalzahl der betreffenden Tonstufe, für die Oktave auf "c" wird zunächst die Grundton-Frequenz als Quotient aus der Kammerton-Frequenz "a = 440.0 Hz" und der Dezimalzahl der "großen Sexte" hergeleitet, dann sind alle Tonfrequenzen wiederum die Produkte aus Grundtonfrequenz und Dezimalzahl.
Zwei verschiedene Frequenzbeispiele sind genannt, um die Unabhängigkeit der Intervallverteilung bei den musikalischen Temperaturen von bestimmten Tonfrequenzen zu belegen.

> Die beiden Kennlinien - "Kennlinie 1" in chromatischer Anordnung, "Kennlinie 2" in der Quintenfolge - zeigen die Differenzen, mit denen die einzelnen Tonstufen von der Gleichstufigkeit abweichen: Es ist für jede Tonstufe der Abstand des Centwertes zu dem entsprechenden 100er-Wert (siehe T 31) von einer Null-Linie aufgetragen und die Verbindungslinie der so gewonnenen Punkte hergestellt.

Das "Profil der musikalische Temperatur" ist auch das "Profil des Instrumentes", wenn ein Instrument mit festen Tonhöhen wie Klavier oder Orgel in dieser musikalischen Temperatur eingestimmt ist.

Das >Profil< macht deutlich, wie sich bei Modulationen von einer Tonart in eine andere in den Tonleitern die Intervallverhältnisse ändern, wenn eine der möglichen anderen Tonstufen als die Ausgangstonstufe benutzt wird.

Für jede der zwölf Tonstufen ist berechnet, wie groß die Differenz zu den in der Grundton-Einstimmung festgelegten Tonleiter-Intervallen ist. Im Diagramm sind in der Horizontalen wie in der Vertikalen die Tonstufen in der Folge des Quintenzirkels angeordnet, die Zahlenangaben sind Centwerte. Ein umlaufender Saum aus lauter Null-Abweichungen ist bei allen Profilen, weil in der Grundtonleiter (auf c) wie auch bei allen elf anderen Tonleitern sowohl bei den elf Grund- und Oktaven-Tonstufen die Centwerte der gewählten musikalischen Temperatur benutzt werden.